Thiết lập phương trình Euler động cho chất lỏng lý tưởng

Trong bài trước chúng ta đã đi tìm hiểu cách thiết lập phương trình Euler tĩnh khi nghiên cứu thủy tĩnh học, và từ phương trình Euler tĩnh chúng ta đã xây dựng được các phương trình cơ bản giúp cho quá trình nghiên cứu và giải bài tập thủy tĩnh học.
Trong bài hôm nay chúng ta sẽ đi tìm hiểu cách thiết lập phương trình Euler động, cũng từ phương trình Euler động ta đi xét một trường hợp riêng từ đó thiết lập phương trình Bernoulli cho chuyển động của chất lỏng lý tưởng.

Nhắc lại khái niệm chất lỏng lý tưởng và chất lỏng thực:

Chất lỏng lý tưởng là chất lỏng mà khi nó chuyển động không xuất hiện ma sát trong lòng chất lỏng, cũng như ma sát chất lỏng với thành ống dẫn, hay thành bình.

Chất lỏng thực là chất lỏng khi mà khảo sát chuyển động của nó phải kể tới sự tác động của nội ma sát và ngoại ma sát.

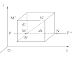
Trong dòng chất lỏng lý tưởng lấy một điểm M bất kỳ có tọa độ là x, y, z và từ điểm đó tách ra một phần chất lỏng có dạng hình hộp chữ nhật, sao cho điểm M là một đỉnh của hình hộp chữ nhật đó, và các cạnh của hình hộp chữ nhật song song với các trục tọa độ (hình vẽ). Kích thước của hình hộp chữ nhật là δx, δy, δz.

Chúng ta thiết lập phương trình chuyển động của khối chất lỏng được tách ra này. Coi nó như một vật rắn có khối lượng m=ρδxδyδz. Tương tự như trong bài: Thiết lập phương trình Euler tĩnh, ta phải kể ra lần lượt các lực tác dụng lên khối chất lỏng này bao gồm: Tổng hợp lực khối từ các thành phần lực theo các trục Ox, Oy, và Oz. Mà các thành phần lực khối này được tính bằng khối lượng khối chất lỏng nhân với lực khối đơn vị tương ứng X, Y, Z. Giả sử áp suất tại điểm M là p, tương tự như trong bài: Thiết lập phương trình Euler tĩnh, áp lực tổng hợp tác dụng lên 2 mặt bên vuông góc với trục Ox của khối chất lỏng là:

${F_{ax}} = - \frac{{\partial p}}{{\partial x}}\delta x\delta y\delta z$

Lực khối thành phần trên Ox:

F_kx= ρδxδyδzX

Gọi v là vận tốc chuyển động của chất lỏng tại điểm M. Vận tốc v có các thành phần theo các phương Ox, Oy, Oz là v_x, v_y, v_z. Khi đó gia tốc hình chiếu theo các trục là dv_x/dt, dv_y/dt, dv_z/dt.

Giả sử kích thước các cạnh hình chữ hộp đủ nhỏ để coi khối chất lỏng như chất điểm M có khối lượng m chuyển động với gia tốc a_x. Lực quán tính tác dụng lên chất điểm M là:

F_qtx= – ma_x = – mdv_x/dt .

Theo nguyên lý Đalămbe ta có hệ lực cân bằng theo phương Ox:

F_ax+ F_kx+ F_qtx= 0

Ta có:

$- \frac{{\partial p}}{{\partial x}}\delta x\delta y\delta z + \rho \delta x\delta y\delta zX - \rho \delta x\delta y\delta z\frac{{d{v_x}}}{{dt}} = 0$

Tương tự trên các phương Oy và Oz ta có:

$- \frac{{\partial p}}{{\partial y}}\delta x\delta y\delta z + \rho \delta x\delta y\delta zY - \rho \delta x\delta y\delta z\frac{{d{v_y}}}{{dt}} = 0$

$- \frac{{\partial p}}{{\partial z}}\delta x\delta y\delta z + \rho \delta x\delta y\delta zZ - \rho \delta x\delta y\delta z\frac{{d{v_z}}}{{dt}} = 0$

Khi đó ta có:

$\frac{{d{v_x}}}{{dt}} = X - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}}$

$\frac{{d{v_y}}}{{dt}} = Y - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}}$ (1.1)

$\frac{{d{v_z}}}{{dt}} = Z - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}}$

Hệ phương trình (1.1) chính là hệ phương trình Euler động đối với chuyển động của chất lỏng lý tưởng. Hệ phương trình (1.1) áp dụng đối với chất lỏng có nén hoặc không nén, và cả trong trường hợp lực khối tác dụng lên chất lỏng không chỉ có mỗi trọng lực, mà còn cả lực quán tính.

Tiếp tục biến đổi hệ phương trình (1.1). Với từng phương trình lần lượt nhân 2 về với dx, dy, dz. Rồi cộng theo vế ta được phương trình.

$Xdx + Ydy + Zdz - \frac{1}{\rho }\left( {\frac{{\partial p}}{{\partial x}}dx + \frac{{\partial p}}{{\partial y}}dy + \frac{{\partial p}}{{\partial z}}dz} \right)$ $= \frac{{d{v_x}}}{{dt}}dx + \frac{{d{v_y}}}{{dt}}dy + \frac{{d{v_z}}}{{dt}}dz$ (1.1a)

Mà ta lại có: dx/dt=v_x; dy/dt=v_y; dz/dt=v_z.

Và vi phân toàn phần:

$dp = \frac{{\partial p}}{{\partial x}}dx + \frac{{\partial p}}{{\partial y}}dy + \frac{{\partial p}}{{\partial z}}dz$

Nên phương trình (1.1a) thành:

$Xdx + Ydy + Zdz - \frac{{dp}}{\rho } = {v_x}d{v_x} + {v_y}d{v_y} + {v_z}d{v_z}$ (1.1b)

Mặt khác ta có:

${v^2} = v_x^2 + v_y^2 + v_z^2$

Lấy đạo hàm 2 vế ta được :

$d{v^2} = d(v_x^2 + v_y^2 + v_z^2) = 2({v_x}d{v_x} + {v_y}d{v_y} + {v_z}d{v_z})$

Thế vào phương trình (1.1b) ta được:

$Xdx + Ydy + Zdz = \frac{{dp}}{\rho } + \frac{{d({v^2})}}{2}$

Hay:

$\rho (Xdx + Ydy + Zdz) = d\left( {p + \frac{{\rho {v^2}}}{2}} \right)$ (1.2)

Xét trường hợp X=Y=0; Z= – g. Đây là trường hợp chất lỏng chuyển động trong môi trường chỉ chịu tác động của lực khối là trọng lực.

Khi đó phương trình (1.2) trở thành dạng:

$- \rho gdz = d\left( {p + \frac{{{v^2}}}{2}} \right)$

Tương đương với:

$d\left( {\frac{p}{{\rho g}} + \frac{{{v^2}}}{{2g}} + z} \right) = 0$

Lấy tích phân trên ta thu được phương trình:

$\frac{p}{{\rho g}} + \frac{{{v^2}}}{{2g}} + z = const$

Đây chính là phương trình Bernoulli dành cho chất lỏng lý tưởng. Các bạn có thể tìm hiểu thêm bài “Phương trình Bernoulli dành cho chất lỏng lý tưởng”.

Điểm 4.6/5 dựa vào 87 đánh giá

SmartPay : Mở ví điện tử đơn giản tiện lợi Click xem
Pierre Cardin : Sale off cuối năm 50% Click xem
MB Android : Miễn phí chuyển khoản tới tất cả các ngân hàng Click xem